链表（List）作为最基础的抽象数据类型（ADT）之一，是学习数据结构的过程中最先学习的一批ADT，同时其在相关的算法题中也有相当重要的地位，需要投入较多的精力去学习。

本博客将介绍单链表，双链表以及循环链表，并给出以C和Java的代码实现，最后还会介绍链表在实际问题中的简单应用。

单链表

单链表的定义和原理

在之前的学习当中，我们可能接触到的最复杂的数据结构就是数组，也就是所谓的线性表，线性表在物理内存上按照顺序邻接储存，这也就导致线性表的插入操作可能需要移动大量的数据，进行大量的操作，这在很多情况下是不可接受的，那么，什么样的数据组织形式可以让我们方便而高效在一串数据中插入内容呢？

经过观察可以发现，线性表的问题在于数据邻接储存导致在插入的过程中需要大量的操作，如果数据不是邻接储存而是在内存中随机分布，是否就可以方便的进行插入呢？答案是肯定的。这样又带来了另外一个问题，应该如何定位某一个数据的下一个数据呢？如果将这一个数据和下一个数据的位置一并储存在一起，找到这个数据也就可以定位下一个数据，如果将这些数据串在一起，知道第一个数据的位置，就可以定位下一个数据，直到找到最后一个数据，通过这样的方式，完成了数据的分布式储存，这样的数据结构，也就是链表。

链表

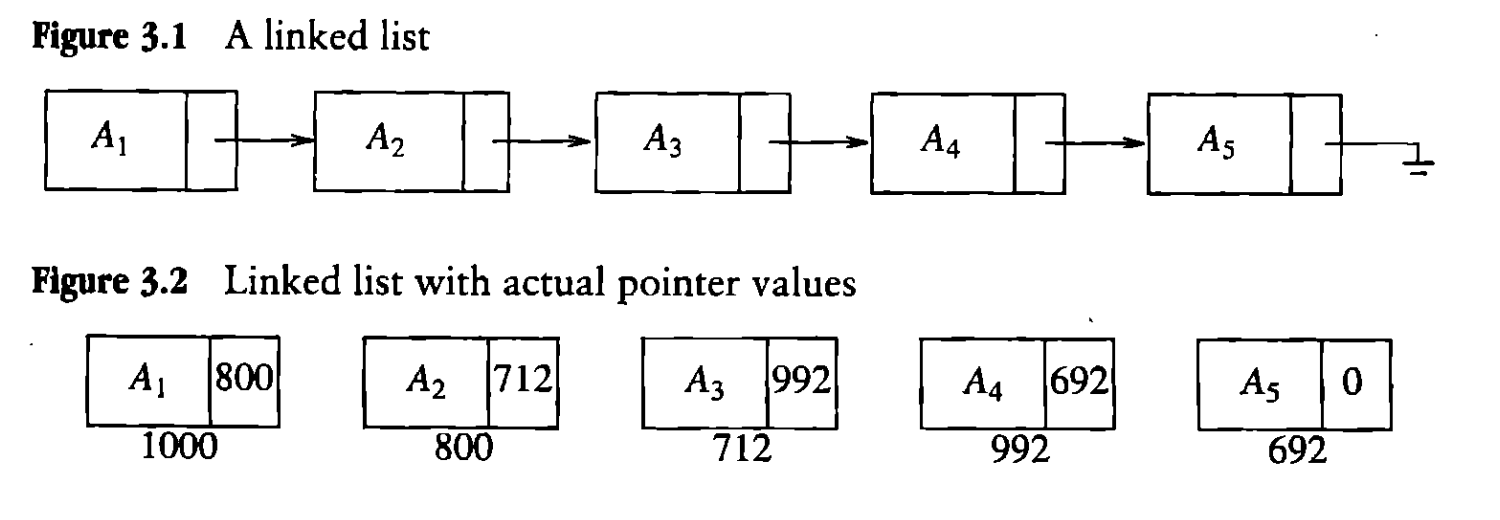
链表中的每一个元素，我们称其为一个结点，在上述的数据结构中，每一个结点都包含这个结点所需要储存的数据以及下一个结点的地址，这样的链表被称为单链表。在图3.2中，如果知道第一个结点的地址“1000”，就可以最终找到链表中的每一个元素，如果这个地址丢失，也就会失去访问整个链表的能力。

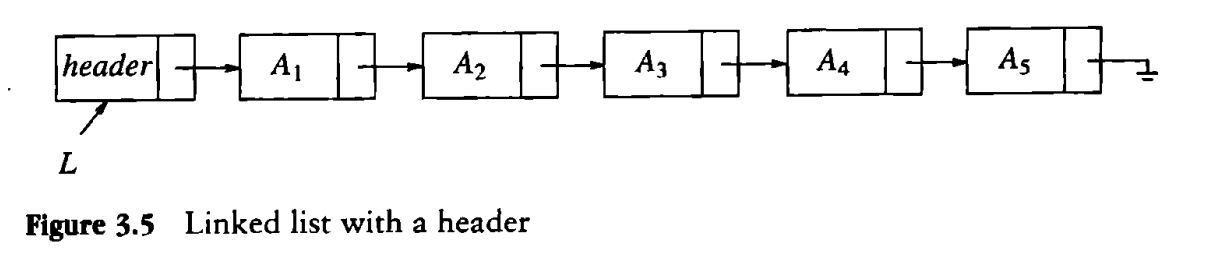
在实际的操作中，可能在第一个结点中储存数据会对操作带来不便，因此，在所有的数据节点前创建一个头结点是一个很常见的操作，这个结点不储存数据，只要头节点的地址不丢失，也就不会丢失整个链表，单链表部分接下来的演示都会基于带头结点的单链表。

带头结点的单链表

单链表结点的定义与创建

通过上述原理的解释，可以认识到，如果要通过链表储存数据，就必须要创建结点，结点是链表中的最小单元。

C实现

用C实现的部分，我刻意避免引入C++的特性。虽然在西电的考试OJ平台上可以上传C++代码，但是将C和C++特性混用在我看来是不能接受的，因此我完全使用了C程序。

1
2
3
4
5
6
typedef struct Node
{
    Type item;
    int length;
    struct Node *next;
}Node, *ListNode;

结点的定义中包括了三个元素，该结点储存的内容，链表的长度以及下一个结点的指针。注意，这里声明了Node为Node类型变量，ListNode为Node*类型的变量，通过这样的声明，在定义一个新结点并为结点分配内存空间时，可以方便的使用ListNode和Node来表示结点的地址类型以及结点本身，提高了程序的可读性。

1
2
3
4
5
6
7
8
ListNode initNode(Type i)
{
    ListNode T = (ListNode)malloc(sizeof(Node));
    if (!T) exit(0);
    T->item = i;
    T->next = NULL;
    return T;
}

初始化结点，也就是创建一个新的结点，需要为一个新的Node类型变量分配空间，鉴于在创建链表、在向头部和尾部添加元素和插入元素都需要创建新的结点，因此将初始化结点抽象为一个函数。
在这个函数中，首先创建了一个新的ListNode型变量T，并为其分配空间，变量T储存了头结点的地址，如果T返回为NULL，说明分配空间失败，接下来，将Type型变量i储存到T结点中，并将T结点的后继节点地址赋值为NULL，这样就完成了节点的初始化。

Java实现

用Java实现的部分，在SLList类中建立private的Node类，这个类不应该被暴露而只被SLList类内部使用。Node类中包含两个成员变量和两个构造方法，两个成员变量分别储存了这个结点的内容和下一个结点的引用，而构造方法分别创建了空和非空的两个结点。构建空节点的主要是在初始化链表的过程当中，可以更加高效创建头节点，剩余的部分和以C实现的原理相同，在此不再赘述。在Java中，通过new关键字创建一个新的Node对象实例，无需手动为其分配内存，也无需手动将结点释放。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class SLList<Type> {
    private class Node {

        private Type item;
        private Node next;

        private Node(Type i, Node p) {
            item = i;
            next = p;
        }

        private Node(Node p) {
            next = p;
        }
    }
}

单链表的初始化和销毁

完成了结点的创建后，接下来就是链表的初始化和销毁，对于单链表来说，就是创建一个空的头结点。

C实现

在C中初始化一个带头结点的单链表和创建一个新结点的差异较小，为了后续的操作方便，在头结点中储存了整个链表的长度，初始化时只有一个空的头结点，链表长度为0。

1
2
3
4
5
6
7
8
ListNode initList(ListNode L)
{
    L = (ListNode)malloc(sizeof(Node));
    if (!L) exit(-1);
    L->next = NULL;
    L->length = 0;
    return L;
}

要销毁一个带头结点的单链表，需要遍历整个链表，逐个删除结点，在释放每一个结点前，都需要创建一个临时结点，储存要被释放的这一结点的后继结点。这样的销毁方式会连同头结点一并销毁，无法再利用这一链表进行相关操作，必须重新初始化。

1
2
3
4
5
6
7
8
9
void deleteList(ListNode L)
{
    while (L != NULL)
    {
        ListNode T = L->next;
        free(L);
        L = T;
    }
}

Java实现

在SLList类中创建sentinel成员变量以及size成员变量，分别为头结点以及链表长度，SLList类的构造器中，将头结点初始化为一个空结点，同时链表长度赋值为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class SLList<Type> {
    /**
     * The sentinel Node.
     */
    private Node sentinel;

    /**
     * Store the size of the queue.
     */
    private int size;

    /**
     * The constructor of an empty queue.
     */
    public SLList() {
        sentinel = new Node(null);
        size = 0;
    }
}

Java中垃圾回收（Garbage Collection）这一机制会自动完成链表的销毁，不需要手动执行这一操作。

单链表的添加，插入和删除

原理

对单链表进行插入和删除操作是非常容易的（在链表头尾添加本质上为特殊的插入）。
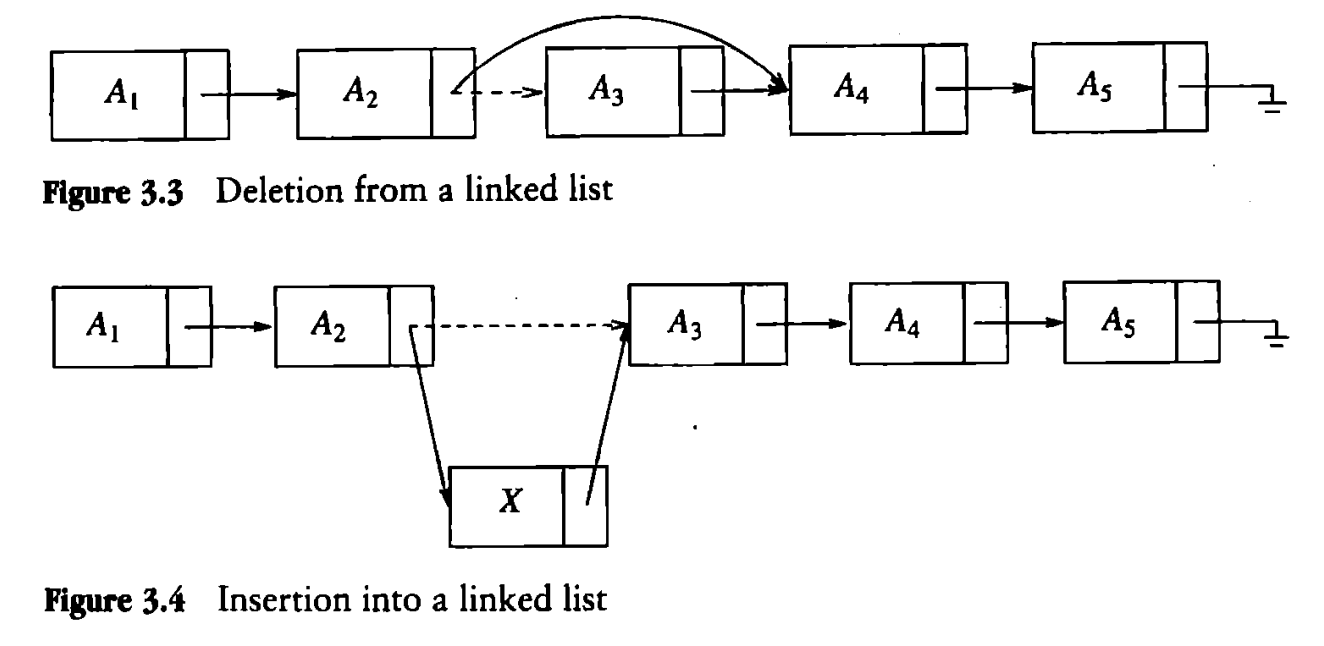
在图3.3中，需要删除节点A3，只需要将A2的后继节点改为A4，就可以将A3从链表中删除。
在图3.4中，若要在A2与A3之间插入节点X，只需要将X的后继节点改为A3，A2的后继节点从A3改为X,即可完成插入（注意顺序！）。

单链表的插入与删除

C实现

在带头结点的单链表的头部插入结点是最简单的操作，初始化一个储存了需要插入数据的结点，将这个结点的后继改为原链表的第一个元素，头结点的后继改为这个结点，即可完成插入。

1
2
3
4
5
6
7
8
9
10
void addFirst(ListNode L, Type i)
{
    //Init a temp node T to store item.
    ListNode T = initNode(i);

    // Insert the node.
    T->next = L->next;
    L->next = T;
    L->length += 1;
}

在带头结点的单链表的尾部插入结点较为繁琐，需要遍历整个链表到达最后一个结点。如果链表非常长，这一操作将会消耗较多的时间，针对这一问题，可以对单链表进行一定的修改，以达到目的，双链表以及循环链表都是可行的修改方式。
由于需要遍历链表，必须要创建一个临时的指针用于遍历，而非直接使用原链表的头指针，否则，遍历完成后将会丢失头节点的位置，无法记录链表长度的变化情况。
C语言中，传入的只是头结点的地址，如果不记录链表长度的变换，可以不创建临时指针进行遍历，并不会影响链表，但如果使用了C++中的引用这一特性，传入的是头结点的引用而非地址，直接使用传入的原链表头指针进行遍历，会导致丢失整个链表！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void addLast(ListNode L, Type i)
{
    // Store the sentenal of the list.
    ListNode P = L;

    // Init a temp node T to store item.
    ListNode T = initNode(i);

    // Iteration to the end of the list.
    while (P->next != NULL)
    {
        P = P->next;
    }

    // Insert the node.
    T->next = P->next;
    P->next = T;
    L->length += 1;
}

在特定位置插入原理与在尾部插入一致，都为在数组中遍历，在指定位置插入即可，只需注意指针移动的次数，以及插入的位置是否超出范围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void insert(ListNode L, Type i, int n)
{
    // Store the sentenal of the list.
    ListNode P = L;

    //Init a temp node T to store item.
    ListNode T = initNode(i);

    if (n-1 > L->length)
    {
        exit(-1);
    }

    // Iteration to the specific position of the list.
    while (n-1 > 0)
    {
        P = P->next;
        n -= 1;
    }
    
    // Insert the node.
    T->next = P->next;
    P->next = T;
}

删除结点的原理也一致，在此不再赘述，注意判断要删除的位置是否大于链表长度即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void Delete(ListNode L, int n)
{
    // Store the sentenal of the list.
    ListNode P = L;

    if (n > L->length)
    {
        exit(-1);
    }

    // Iteration to the specific position of the list.
    while (n-1 > 0)
    {
        P = P->next;
        n -= 1;
    }
    
    // Free the node.
    ListNode T = P->next;
    P->next = P->next->next;
    free(T);
}

Java实现

Java实现只给出在链表的头部以及尾部的插入与删除，原理一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void addFirst(Type i) {
    Node newNode = new Node(i, sentinel.next);
    sentinel.next = newNode;
    size += 1;
}

public void addLast(Type i) {
    Node n = sentinel;
    while (n.next != null) {
        n = n.next;
    }
    Node newNode = new Node(i, n.next);
    n.next = newNode;
    size += 1;
}

单链表的查找打印以及其他操作

双链表

循环链表

链表的简单运用

一元多项式的计算

约瑟夫问题